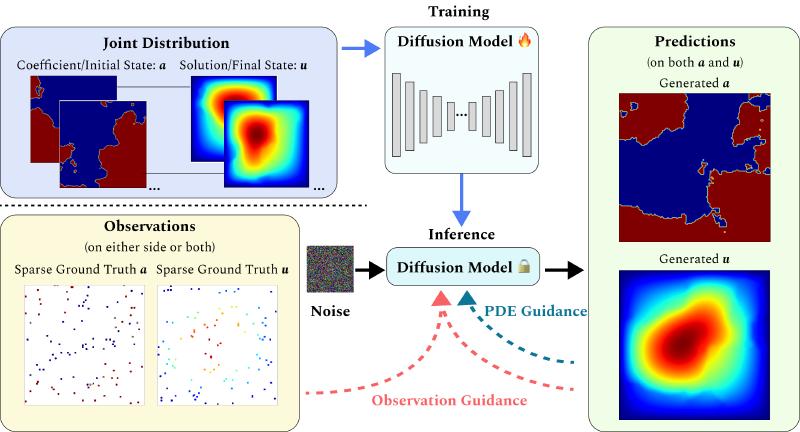
The new framework, DiffusionPDE, tackles a fundamental challenge in scientific computing: how to accurately solve PDEs when we don’t have complete knowledge of all the variables needed to solve the equation fully.
DiffusionPDE
Unlike traditional PDE solvers that struggle with scenarios such as: Incomplete boundary conditions: When you don’t know the values or constraints at all boundaries of your domain. Sparse measurements: When you only have data at certain points or regions rather than throughout the entire domain. Uncertain coefficients: When the physical properties (like diffusivity, permeability, or conductivity) that appear as coefficients in the PDE are not fully known across the domain. Missing initial conditions: When you lack complete information about the state of the system at the starting time. Partial geometry: When parts of the computational domain itself are not fully specified. DiffusionPDE leverages generative diffusion models to simultaneously fill in missing data and solve the equations by modeling the joint distribution of solution and coefficient spaces.The applications are tremendously exciting across multiple fields:
Applications
Geophysics
Enhancing seismic imaging with sparse sensor data: Need for PDEs: Geophysical exploration depends heavily on wave propagation and diffusion processes to interpret subsurface structures.Examples of PDEs:Acoustic Wave Equation: Used in modeling pressure waves in the Earth for seismic imaging.Elastic Wave Equation: Captures the behavior of shear and compressional waves in elastic media, essential for interpreting seismic data.Diffusion Equation: Applied in groundwater flow models and for simulating heat distribution in the subsurface.
Medical Imaging
Improving reconstruction from limited MRI/CT views :Need for PDEs: In medical imaging modalities, PDEs are employed to reconstruct internal body structures from limited or noisy data and to simulate physiological processes.Examples of PDEs:Heat/Diffusion Equation: Governs thermal diffusion in tissues and is crucial for thermal imaging and hyperthermia treatment planning.Reaction-Diffusion Equations: Model tissue growth, tumor progression, or the spread of contrast agents in imaging.Maxwell’s Equations (in a PDE form): Underpin electromagnetic imaging techniques such as MRI and electrical impedance tomography.
Environmental Monitoring
Filling gaps in satellite imagery for climate modeling:Need for PDEs: Environmental processes such as pollutant transport or climate dynamics are described by PDEs, despite the challenge of incomplete spatial or temporal data.Examples of PDEs:Advection-Diffusion Equation: Models the transport of pollutants in air or water, accounting for both convection and diffusion.Shallow Water Equations: Describe the flow dynamics in rivers, lakes, and coastal areas, essential for flood forecasting and ocean modeling.Radiative Transfer Equations: Govern the propagation of radiation through the atmosphere, critical for satellite-based climate monitoring.
Industrial Inspection
Detecting material flaws from partial measurements:Need for PDEs: PDEs are used to simulate the behavior of materials and detect anomalies from limited sensor data during the inspection processes.Examples of PDEs:Wave Equation: Used in ultrasonic testing to predict the propagation of elastic waves for detecting structural defects.Heat Conduction/Diffusion Equation: Applied in thermal imaging techniques to identify flaws through temperature distribution patterns.Electrical Potential Equations: Underlie methods such as eddy-current testing, where variations in electrical fields can indicate material imperfections.
Atmospheric Science
Refining weather predictions with incomplete global data:Need for PDEs: Climate models require solving complex PDEs that represent fluid dynamics, energy transfer, and other processes in the atmosphere and oceans.Examples of PDEs:Navier–Stokes Equations: Fundamental for simulating fluid flows in the atmosphere and oceans.Primitive Equations: Simplified forms of the full Navier–Stokes equations used in global circulation and weather forecasting models.Energy Balance and Radiative-Convective Equations: Model the energy exchange within the climate system, including radiative transfer and heat conduction.
Astrophysics
Modeling cosmic phenomena from limited observational inputs:Need for PDEs: Astrophysical phenomena often involve extreme conditions and complex interactions that are described by coupled PDE systems.Examples of PDEs:Magnetohydrodynamics (MHD) Equations: Describe the dynamics of plasma in astrophysical environments, combining fluid dynamics with magnetic field interactions.Radiative Transfer Equations: Essential for modeling the propagation of light through stellar atmospheres and interstellar media.Gravitational Field Equations (e.g., Poisson’s Equation): Used in modeling gravitational potentials in galaxies and clusters.Einstein Field Equations: Describe the dynamics of spacetime in the context of general relativity, applicable to black hole and cosmological studies.What makes this approach powerful is its ability to significantly outperform state-of-the-art methods in both forward and inverse problem-solving directions by incorporating learned generative priors.For those working in computational science or AI for scientific applications, this paper represents an important advancement in combining data-driven approaches with physical modeling.